Dầm thép gá»m những tấm má»ng ghép vá»i nhau. Äá» giảm nhẹ trá»ng lượng dầm và táºn dụng khả nÄng của váºt liá»u, cần táºn dụng các tấm má»ng có kÃch thÆ°á»c lá»n. Tấm má»ng chá»u lá»±c trong mặt phẳng của nó nhÆ° nén, uá»n, trượt có thá» bá» vênh ra ngoà i mặt phẳng của tấm; gá»i là tấm bá» mất á»n Äá»nh. Các ứng suất tÆ°Æ¡ng ứng suất tá»i hạn vá» nén, uá»n, trượt.
Tấm bá» vênh, bá» mất á»n Äược gá»i Äá»nh cục là ứng bá», nói chung không là m mất khả nÄng chá»u lá»±c của dầm. NhÆ°ng sẽ thay Äá»i sá»± là m viá»c của toà n kết cấu, và dụ dá»n lá»±c ra các phần còn á»n Äá»nh, nên nói chung là không Äược phép (hình 3.29).
Tấm má»ng trong cấu kiá»n dầm và cá»t có các dạng ứng suất sau:
- Nén Äá»u theo má»t phÆ°Æ¡ng: trong bụng hay cánh cá»t nén Äúng tâm;
- Nén không Äá»u hoặc kéo nén trong mÄt phẳng tấm: bụng cá»t nén lá»ch tâm, bụng dầm;
- Trượt thuần túy tác dụng theo chu vi bụng dầm
- Hoặc Äá»ng thá»i có cả các loại nà y
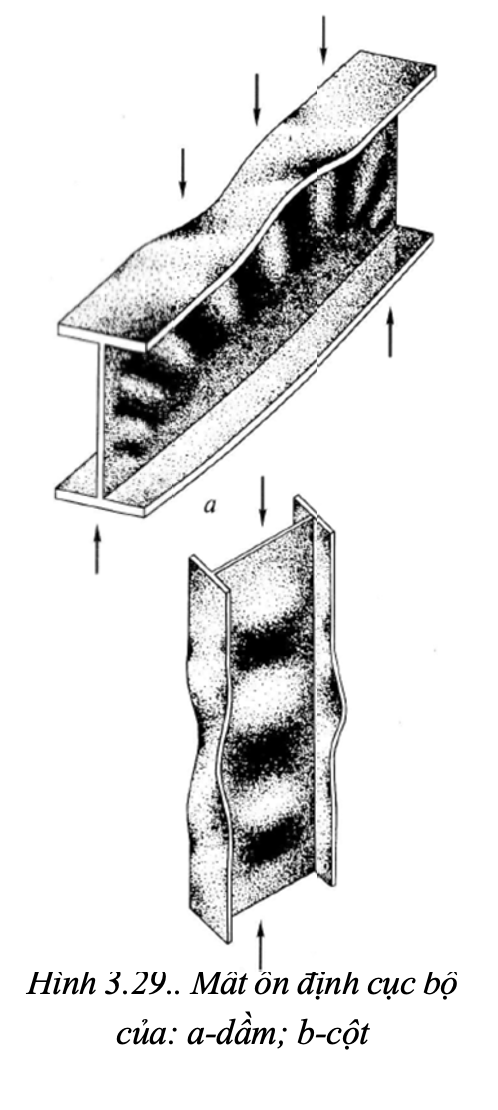
Khi ứng suất vượt trá» sá» tá»i hạn, tấm bá» mất á»n Äá»nh hiá»u theo nghÄ©a chung nhÆ°: xuất hiá»n dạng cân bằng má»i khác vá» chất, hoặc công của ná»i lá»±c không thá» cân bằng vá»i công của ngoại lá»±c.
Còn trạng thái tá»i hạn Äạt Äược khi công ngoại lá»±c bằng công ná»i lá»±c ï¤Ai ï½ ï¤Ae . Xét má»t tấm chiá»u dà i a, chiá»u rá»ng b, dà y t, á» biên liên kết khá»p chá»u tải trá»ng phân bá» Äá»u N (hình 3.30).
Tấm vênh sóng hình sin, PhÆ°Æ¡ng trình vi phân chuyá»n vá» ra ngoà i mặt phẳng của tấm có dạng sau:

Vá»i những tấm có hình dạng, Äiá»u kiá»n liên kết biên và tải trá»ng khác, (3.55) chá» cần thay Äá»i há» sá» k. Các và dụ có thá» xem trong [21], [22].
Thay giá trá» D và o (3.55), có ứng suất tá»i hạn của tấm:

Cánh dầm chữ I. SÆ¡ Äá» tÃnh là má»t tấm dà i, có chiá»u dà y t=tf và bá» rá»ng b=bef, liên kết khá»p dá»c theo má»t cạnh dà i, cạnh dà i còn lại tá»± do.
Tấm chá»u nén Äá»u theo cạnh ngắn N=ï³.tf, ï³=M/W (hình 3.31). Theo nghiên cứu của Timosenko, trong giai Äoạn là m viá»c Äà n há»i của váºt liá»u giá trá» k trong (3.55) k ï½ 0,456 ï« b2 / a2 . Khi a>>b có k=0,456, giá trá» ï¬uf ï½ 0,95 ï½ 0,64. Thá»±c tế, trong dầm tá» hợp liên kết hà n, cánh luôn có dạng cong ngẫu nhiên (dạng nấm của má»i hà n liên kết cánh), lá»±c tá»i hạn thá»±c tế sẽ bá» giảm so vá»i lý thuyết trên.

Nếu dầm là m viá»c trong giai Äoạn Äà n há»i dẻo, cánh dầm trong trạng thái dẻo. Trong trÆ°á»ng hợp nà y Äá» mảnh giá»i hạn giảm xuá»ng ï¬uf ï½ 0,3 . Theo tiêu chuẩn á»n Äá»nh cục bá» cánh dầm, là m viá»c trong giai Äoạn Äà n dẻo, xác Äá»nh từ Äiá»u kiá»n á»n Äá»nh Äá»u cả cánh và bụng. Vá»i chiá»u cao bụng h=hw, chiá»u dà y t=tw. Khi hai cạnh bản bụng liên kết khá»p k=23,9, có ï¬ uw ï½ 0,95ï½ 4,64 . Bụng liên kết không hoà n toà n vá»i cánh, tiêu chuẩn lấy ï¬uw ï½ 5,5 . Xét Äến biến dạng dẻo giá trá» Äá» mảnh quy Æ°á»c giá»i hạn bản bụng giảm xuá»ng ï¬ uw ï½ 2,2 . Vì váºy, Äá» mảnh giá»i hạn quy Æ°á»c bản cánh 0,3 ï¼ ï¬ uf ï¼ 0,5 , bản bụng 2,2 ï¼ ï¬ uw ï¼ 5,5 .
Có quan há» giữa Äá» mảnh quy Æ°á»c giá»i hạn bản cánh và bản bụng theo quy luáºt ï¬uf ï½ ï¡ ï« ï¢ï¬uw và sá» dụng phÆ°Æ¡ng pháp giá trá» biên, có ï¡=0,17; ï¢=0.06. Do Äó dầm là m viá»c trong giai Äoạn Äà n há»i dẻo có:
![]()
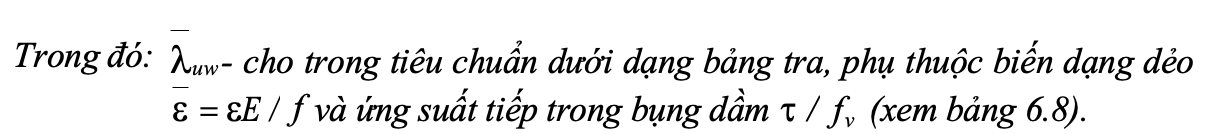
Cánh cá»t chữ I. Mất á»n Äá»nh cục bá» cánh và bụng cá»t, xác Äá»nh từ Äiá»u kiá»n á»n Äá»nh Äá»u các bản thép, và toà n cá»t. á»n Äá»nh cánh và toà n cá»t thá» hiá»n bằng ứng suất tá»i hạn ï³crf ï½ ï³cr . Sá» dụng (3.56) và (3.25), có 0,9kEï¨t f / bef ï© ï½ ïª. f .

Bụng cá»t chữ I. Trong trÆ°á»ng hợp nà y coi mất á»n Äá»nh cục bá» cánh và bụng cá»t là cùng vá»i nhau, từ (3.60) có ï¬uw ï½ 0,95 . Bản bụng cá»t chá»u nén Äúng tâm có thá» sá» dụng sÆ¡ Äá» tÃnh nhÆ° hình 3.30. Khi Äó trong trÆ°á»ng hợp lý tÆ°á»ng giá trá» nhá» nhất k=4 Äạt Äược trong (3.55) là a=b. Thá»±c tế các bản thép tá» hợp thà nh cá»t vẫn có sai lá»ch kÃch thÆ°á»c hình há»c, do Äó ứng suất tá»i hạn sẽ Äược giảm khi có sá»± phát triá»n biến dạng dẻo, trong tiêu chuẩn cho 2ï£ k ï£3,7. TÆ°Æ¡ng tá»± phần trÆ°á»c, phụ thuá»c và oïª( ï¬ ), có Äá» mảnh giá»i hạn của bản bụng bụng cá»t chá»u nén Äúng tâm

Bụng dầm chữ I (hình 3.32). Xét má»t sá» trÆ°á»ng hợp sau:
a. à bản giữa dầm có thá» mất á»n Äá»nh bá»i ứng suất pháp ï³=max, ứng suất tiếp ï´=0. Nhân và tách vế phải (3.56) vá»i f, thay b=hw, t=tw, có

Tiêu chuẩn cho giá trá» ï¢ =ï¥ (có nghÄ©a k2=ï¥) khi cánh nén liên kết vá»i sà n cứng, ï¢ =2 khi ray cầu chạy không hà n vá»i cánh nén, các trÆ°á»ng hợp còn lại ï¢= 0,8.
Khi liên kết giữa cánh và bụng là ngà m Äà n há»i, giá trá» ccr phụ thuá»c và o ï¤, nằm trong giá»i hạn 30ï£ccrï£35,5.
b. à bản tại gá»i có ứng suất pháp ï³=0, ứng suất tiếp ï´=max. SÆ¡ Äá» tÃnh nhÆ° hình 3.33. DÆ°á»i tác dụng của ứng suất tiếp, bản bụng sẽ mất á»n Äá»nh nén theo
ÄÆ°á»ng chéo 2-2. Kéo dá»c theo ÄÆ°á»ng chéo 1-1 sẽ giữ hình dáng thẳng góc.
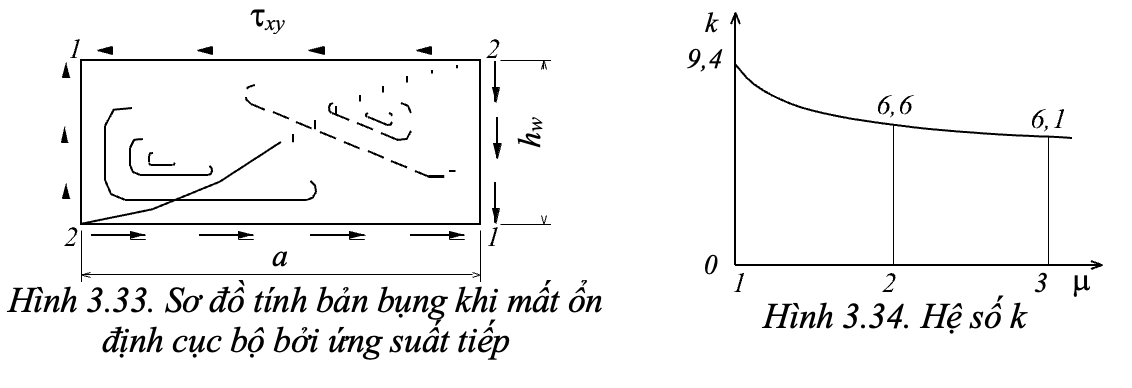
Trong trÆ°á»ng hợp nà y, ứng suất tá»i hạn ï´cr xác Äá»nh nhÆ° công thức (3.56), trong Äó giá trá» k phụ thuá»c tá»· sá» giữa cạnh dà i và cạnh ngắn ï=a/b (hình 3.34). NhÆ° váºy, tÆ°Æ¡ng tá»± công thức (3.65) ta có

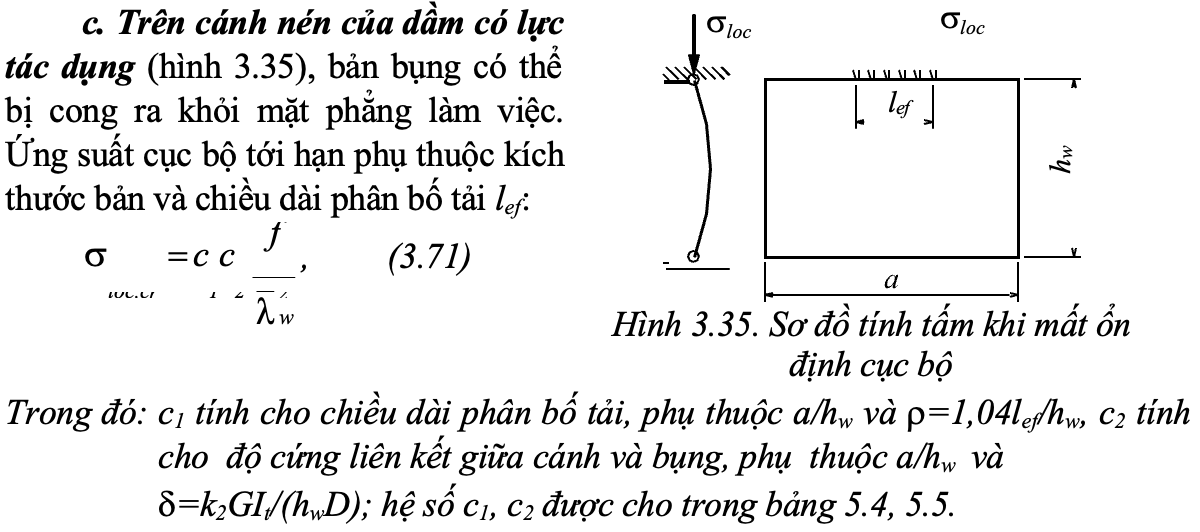
d. Chá»u Äá»ng thá»i ba thà nh phần ứng suất. Trong bản bụng cùng lúc tá»n tại cả mômen, lá»±c cắt, lá»±c táºp trung gây ra các ứng suất thà nh phần , ,ï³loctheo B.M. Broude [16]. Trạng thái giá»i hạn của dầm thép 1953, kiá»m tra ô bản bụng theo mặt lá»i (hình 3.36).
.png)
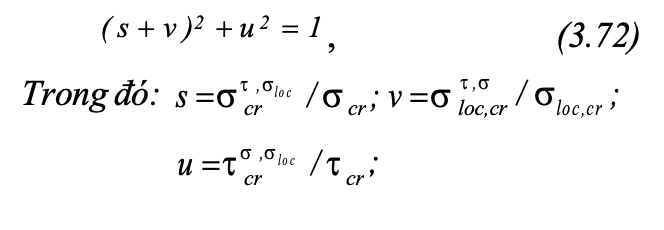
.png)
CÃU Há»I ÃN TẬP CHÆ¯Æ NG 3:
- TÃnh toán kết cấu thép theo phÆ°Æ¡ng pháp trạng thái giá»i hạn ? Sá»± khác nhau giữa phÆ°Æ¡ng pháp tÃnh theo trạng thái giá»i hạn so vá»i các phÆ°Æ¡ng pháp khác là gì ?
- TÃnh toán các cấu kiá»n cÆ¡ bản: chá»u kéo Äúng tâm, chá»u uá»n, chá»u nén Äúng tâm, chá»u kéo lá»ch tâm, chá»u nén lá»ch tâm, cấu kiá»n chá»u xoắn ?
- Sá»± mất á»n Äá»nh tá»ng thá» của cấu kiá»n chá»u uá»n ?
- á»n Äá»nh cục bá» của cấu kiá»n kết cấu thép ?
|
|
